Pi Day

I was inspired to post this by Rhett Allain's work on calculating Pi based upon a random walk. Another method that you can use to calculate Pi based upon random numbers relies upon Monte Carlo Integration of a Unit Circle. Here is a Mac OS X 10.10 and higher executable that you can use to explore the calculation. Increasing the number of guesses, gives you are better value of Pi within the limits of computational error. You can download the Swift 3.0 code for this project here.
Download the updated Swift 4.0 code for this project here.

Two Functions perform the bulk of the work and are reproduced below. The first calculates the value of Pi by taking the ratio of the number of random points within the radius of a Unit Sphere to those outside the radius and multiplying by the area of a bounding box. The second function calculates the total number of points within the the Unit Sphere.

/// calculate the value of Pi /// /// - Calculates the Value of Pi using Monte Carlo Integration /// /// - Parameter sender: Any @IBAction func CalculatePI(_ sender: Any) { var maxGuesses = 0.0 let boundingBoxCalculator = BoundingBox() ///Instantiates Class needed to calculate the area of the bounding box. maxGuesses = displayGuesses.doubleValue totalIntegral = totalIntegral + calculateMonteCarloIntegral(radius: radius, maxGuesses: maxGuesses) totalGuesses = totalGuesses + maxGuesses displayTotalGuesses.doubleValue = totalGuesses ///Calculates the value of π from the area of a unit circle pi = totalIntegral/totalGuesses * boundingBoxCalculator.calculateSurfaceArea(numberOfSides: 2, lengthOfSide1: 2.0*radius, lengthOfSide2: 2.0*radius, lengthOfSide3: 0.0) displayPI.doubleValue = pi displayView.tellGuiToDisplay() } /// calculates the Monte Carlo Integral of a Circle /// /// - Parameters: /// - radius: radius of circle /// - maxGuesses: number of guesses to use in the calculaton /// - Returns: ratio of points inside to total guesses. Must mulitply by area of box in calling function func calculateMonteCarloIntegral(radius: Double, maxGuesses: Double) -> Double { var numberOfGuesses = 0.0 var pointsInRadius = 0.0 var integral = 0.0 var point = (xPoint: 0.0, yPoint: 0.0, radiusPoint: 0.0, color: "Red") while numberOfGuesses < maxGuesses { /* Calculate 2 random values within the box */ /* Determine the distance from that point to the origin */ /* If the distance is less than the unit radius count the point being within the Unit Circle */ point.xPoint = Double.getRandomNumber(lower: -radius, upper: radius) point.yPoint = Double.getRandomNumber(lower: -radius, upper: radius) point.radiusPoint = sqrt(pow(point.xPoint,2.0) + pow(point.yPoint,2.0)) displayView.shouldIDrawPoints = true // if inside the circle add to the number of points in the radius if((radius - point.radiusPoint) >= 0.0){ pointsInRadius += 1.0 point.xPoint = point.xPoint * Double(displayView.frame.width)/2.0 + Double(displayView.frame.width)/2.0 point.yPoint = point.yPoint * Double(displayView.frame.height)/2.0 + Double(displayView.frame.height)/2.0 point.color = "Red" displayView.addPoint(xPointa:point.xPoint, yPointb: point.yPoint, radiusPointc: point.radiusPoint, colord: point.color) } else { //if outside the circle do not add to the number of points in the radius point.xPoint = point.xPoint * Double(displayView.frame.width)/2.0 + Double(displayView.frame.width)/2.0 point.yPoint = point.yPoint * Double(displayView.frame.height)/2.0 + Double(displayView.frame.height)/2.0 point.color = "Blue" displayView.addPoint(xPointa:point.xPoint, yPointb: point.yPoint, radiusPointc: point.radiusPoint, colord: point.color) } numberOfGuesses += 1.0 } integral = Double(pointsInRadius) return integral }

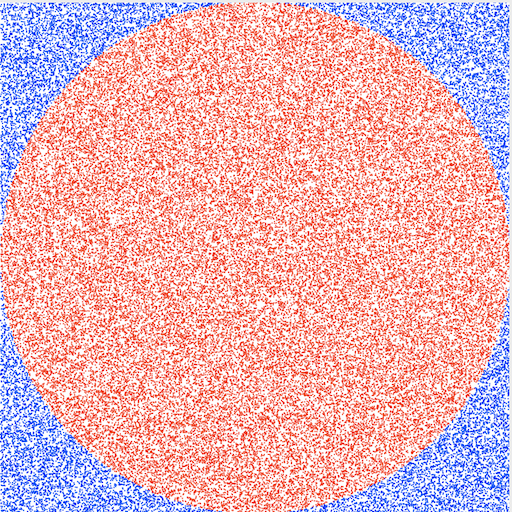Using random numbers to calculate the value of pi by determining the area of a Unit Circle where the Area = pi.